Quelles sont les lois de Kirchhoff ?

Introduction

Brève présentation de Gustav Robert Kirchhoff

Importance des Lois de Kirchhoff en physique et en ingénierie

Les lois de Kirchhoff, formulées dans les années 1840, sont deux règles fondamentales qui régissent le flux de courant électrique dans les circuits. Elles sont indispensables pour l’analyse des circuits électriques, permettant de comprendre comment le courant et la tension se distribuent dans un réseau complexe.

La première loi, connue sous le nom de loi des nœuds, énonce que la somme totale des courants entrant dans un nœud est égale à la somme totale des courants sortant de ce nœud. Cette loi est une conséquence directe de la conservation de la charge électrique.

La seconde loi, la loi des mailles, affirme que la somme des différences de potentiel le long d’une boucle fermée est égale à zéro. Cette loi découle du principe de conservation de l’énergie.

Ces lois sont cruciales non seulement pour les étudiants et les professionnels en physique et en génie électrique, mais elles jouent également un rôle essentiel dans la conception et l’analyse de presque tous les dispositifs électroniques modernes. De l’éclairage domestique aux systèmes de communication avancés, les lois de Kirchhoff restent un pilier fondamental dans le domaine de l’électrotechnique.

Dans les sections suivantes, nous allons explorer en détail chaque loi, en illustrant leur application et leur importance dans divers contextes.

Fondements de l’électrocinétique

Concepts de base : courant, tension, résistance

Avant d’aborder les lois de Kirchhoff, il est essentiel de comprendre les concepts fondamentaux de l’électrocinétique : le courant, la tension et la résistance.

• Le courant électrique est un flux de charges électriques, généralement mesuré en ampères. Il peut être continu (CC) ou alternatif (CA), reflétant la manière dont les charges se déplacent à travers un conducteur.
• La tension est la différence de potentiel électrique entre deux points d’un circuit. Elle détermine la quantité d’énergie potentielle électrique par charge unitaire et est mesurée en volts. La tension est souvent comparée à la « pression » qui pousse les charges à travers un conducteur.
• La résistance est la propriété d’un matériau qui s’oppose au flux de courant. Mesurée en ohms, elle dépend de la composition, de la taille et de la température du conducteur.

Ces trois éléments sont liés par la loi d’Ohm, qui énonce que la tension (V) est égale au produit du courant (I) et de la résistance (R), soit V = IR.

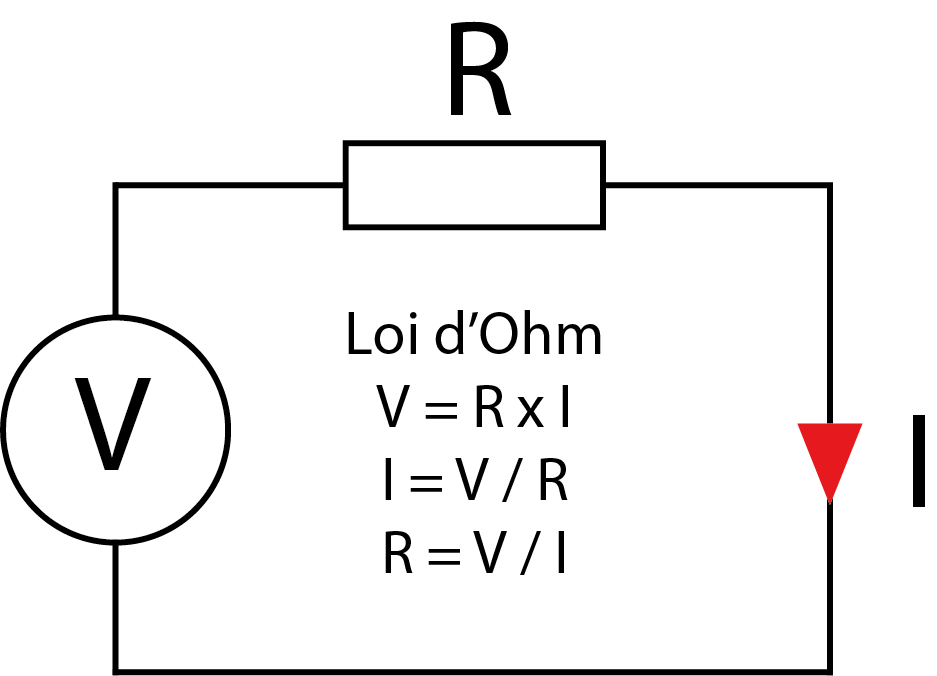
Bref historique de l’électrocinétique

L’électrocinétique, l’étude des charges électriques en mouvement, a évolué significativement depuis ses débuts au 18e siècle. Les premières découvertes, comme celles de Benjamin Franklin et de Michael Faraday, ont jeté les bases de la compréhension moderne de l’électricité.

Au 19e siècle, des scientifiques comme Ohm, Kirchhoff, et Maxwell ont formalisé ces connaissances, menant à la théorie classique de l’électromagnétisme et à la compréhension détaillée des circuits électriques. Les travaux de Kirchhoff, en particulier, ont permis d’établir des règles permettant de calculer les courants et les tensions dans les circuits complexes, une avancée cruciale pour le développement de la technologie électrique.

La compréhension de ces concepts est essentielle pour apprécier pleinement la portée et l’application des lois de Kirchhoff, qui sont abordées dans les sections suivantes de cet article.

La première loi de Kirchhoff : la Loi des Nœuds

Explication de la loi

La première loi de Kirchhoff, également connue sous le nom de loi des nœuds ou loi des courants, est fondamentale pour analyser les circuits électriques. Elle stipule que pour tout nœud dans un circuit électrique, la somme des courants entrant dans le nœud est égale à la somme des courants sortant du nœud. Formulée mathématiquement, cela s’écrit comme suit :

∑ des courants entrants = ∑ des courants sortants​.

Cette loi découle directement du principe de conservation de la charge électrique, indiquant qu’aucune charge n’est perdue ou gagnée à un nœud dans un circuit stable. En d’autres termes, tout ce qui entre dans un nœud doit en sortir.

Applications pratiques et exemples

Dans la pratique, la loi des nœuds est utilisée pour déterminer les valeurs de courant inconnues dans un circuit. Par exemple, si deux courants de 2 A et 3 A entrent dans un nœud, et si un courant de 4 A en sort, alors un autre courant de 1 A doit également sortir du nœud pour maintenir l’équilibre conformément à la loi.

Cette loi est particulièrement utile dans les circuits complexes avec de multiples branches, où elle permet de simplifier l’analyse en se concentrant sur les points de jonction des courants.

Notre sélection de multimètres pour expérimenter

Résolution de problèmes simples

Pour appliquer la loi des nœuds, il est souvent nécessaire de suivre une méthode systématique :

1. Identifier les nœuds : Déterminez tous les points du circuit où deux ou plusieurs composants se rejoignent.
2. Attribuer des directions de courant : Choisissez arbitrairement des directions pour les courants (entrant ou sortant) si elles ne sont pas déjà fournies.
3. Appliquer la Loi des Nœuds : Utilisez l’équation de la loi des nœuds pour établir des relations entre les courants.
4. Résoudre les équations : Utilisez les équations pour trouver les valeurs inconnues des courants dans le circuit.

Cette approche permet de résoudre de nombreux problèmes de circuits, allant des plus simples aux plus complexes, en fournissant un cadre systématique pour l’analyse des courants électriques.

La seconde Loi de Kirchhoff : la Loi des Mailles

Explication de la loi

La seconde loi de Kirchhoff, souvent appelée loi des mailles, s’applique aux boucles fermées d’un circuit électrique. Elle stipule que la somme algébrique des différences de potentiel (tensions) autour de n’importe quelle boucle fermée du circuit est égale à zéro. En termes mathématiques, cela se formule ainsi :

∑ des tensions = 0 pour une boucle fermée.

Cette loi est basée sur le principe de conservation de l’énergie. Elle assure que l’énergie totale gagnée par les charges en parcourant un chemin fermé est équivalente à l’énergie totale perdue, impliquant qu’aucune énergie n’est créée ni détruite dans le circuit.

Applications pratiques et exemples

En pratique, la loi des mailles est utilisée pour calculer les tensions inconnues dans un circuit. Par exemple, si une boucle contient une batterie de 9 V et des résistances à travers lesquelles une chute de tension de 5 V et 3 V est mesurée, la loi des mailles indique qu’il doit y avoir une chute de tension supplémentaire de 1 V quelque part dans la boucle pour que la somme totale des tensions soit égale à zéro.

Cette loi est essentielle pour analyser des circuits plus complexes, en particulier ceux contenant plusieurs boucles et sources de tension, où elle permet d’établir des équations qui lient les différentes tensions du circuit.

Résolution de problèmes simples

Pour appliquer la loi des mailles, suivez ces étapes :

1. Identifier les boucles : Sélectionnez les boucles fermées dans le circuit.
2. Attribuer des directions de tension : Déterminez les directions des tensions (positive ou négative) en suivant un sens de parcours (habituellement dans le sens des aiguilles d’une montre).
3. Appliquer la Loi des Mailles : Écrivez une équation pour chaque boucle en additionnant algébriquement les tensions, en tenant compte de leur signe (positif pour une augmentation de potentiel, négatif pour une diminution).
4. Résoudre les équations : Utilisez les équations établies pour trouver les valeurs inconnues des tensions dans le circuit.

Un exemple concret :

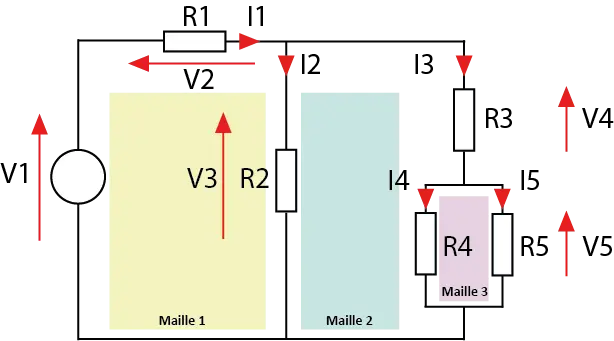
I1 =I2 + I3, I3 = I4 + I5 : illustration de la loi des noeuds
V1 – V2 – V3 = 0, V3 – V4 – V5 = 0 : illustration de la loi des mails

Cette méthode est un outil puissant pour déchiffrer les relations entre différentes tensions dans un circuit, facilitant la compréhension et la résolution de circuits complexes.

Expériences faciles avec un multimètre

Comprendre les Lois de Kirchhoff à l’aide d’exemples

Études de cas détaillées

Pour illustrer l’application des lois de Kirchhoff, examinons quelques études de cas où ces lois sont utilisées pour analyser des circuits.

Exemple 1 : circuit simple avec plusieurs résistances

Imaginons un circuit avec une source de tension et trois résistances en série. En utilisant la loi des mailles, nous pouvons établir une relation entre la tension de la source et les chutes de tension aux bornes de chaque résistance. Cette analyse nous permet de déterminer la tension à travers chaque résistance.

Exemple 2 : circuit avec plusieurs nœuds et boucles

Considérons un circuit plus complexe avec plusieurs nœuds et boucles, incluant des sources de tension et de courant. Ici, la combinaison des deux lois de Kirchhoff nous permet de résoudre le circuit en calculant les courants inconnus et les tensions à travers les composants.

Analyse de circuits simples et complexes

Les lois de Kirchhoff ne se limitent pas à des exemples théoriques simples; elles s’appliquent également à des circuits plus complexes et réalistes.

Circuit avec des branches parallèles

Dans un circuit comportant des branches parallèles, la loi des nœuds peut être utilisée pour déterminer les courants dans chaque branche. Ensuite, la loi des mailles peut être appliquée pour trouver les tensions aux bornes des différents composants.

Circuit avec plusieurs sources de tension

Dans les circuits avec plusieurs sources de tension, la loi des mailles devient cruciale pour déterminer comment ces différentes tensions interagissent et se répartissent dans le circuit.

Importance de la méthodologie

Ces exemples soulignent l’importance d’une approche méthodique lors de l’analyse de circuits. Identifier correctement les nœuds, les boucles, et appliquer systématiquement les lois de Kirchhoff permet de résoudre des circuits qui, autrement, seraient trop complexes pour être abordés intuitivement.

Importance des Lois de Kirchhoff dans les technologies modernes

Applications dans la conception de circuits

Les lois de Kirchhoff ne sont pas seulement des outils théoriques ; elles jouent un rôle crucial dans la conception et l’analyse de circuits électroniques modernes. Que ce soit pour des dispositifs aussi simples que des éclairages domestiques ou aussi complexes que des systèmes informatiques, ces lois fournissent le cadre nécessaire pour comprendre et prédire le comportement des circuits électriques.

• Conception de Circuits Imprimés (PCB) : Les ingénieurs utilisent les lois de Kirchhoff pour optimiser la disposition et la connectivité des composants sur les PCB, assurant ainsi une distribution efficace du courant et minimisant les interférences.
• Systèmes Électroniques Intégrés : Dans les systèmes intégrés comme les smartphones ou les ordinateurs, où l’espace et l’efficacité énergétique sont primordiaux, appliquer ces lois permet d’optimiser la consommation d’énergie et la performance des circuits.

Rôle dans l’avancement de l’électronique

Les lois de Kirchhoff ont également joué un rôle important dans l’avancement de l’électronique et de la technologie.

• Développement de nouveaux composants : La compréhension des lois de Kirchhoff est essentielle pour développer de nouveaux composants électroniques, tels que les semi-conducteurs, les transistors et les diodes, qui sont les pierres angulaires de l’électronique moderne.
• Innovation dans l’énergie renouvelable : Dans le domaine de l’énergie renouvelable, notamment les systèmes solaires et éoliens, ces lois aident à concevoir des systèmes de gestion de l’énergie plus efficaces et fiables.

Applications pratiques au quotidien

Les lois de Kirchhoff trouvent leur application dans de nombreux aspects de la vie quotidienne.

• Diagnostique de problèmes de circuit : Les techniciens et les ingénieurs s’appuient sur ces lois pour diagnostiquer et résoudre des problèmes dans divers appareils électriques.
• Éducation et formation : Ces lois sont un élément fondamental de l’enseignement en ingénierie électrique, offrant aux étudiants les bases nécessaires pour comprendre et concevoir des systèmes électriques complexes.

Défis et limitations des Lois de Kirchhoff

Limites d’application

Bien que les lois de Kirchhoff soient extrêmement utiles, elles ont certaines limitations qu’il est important de reconnaître :

• Circuits à haute fréquence : Dans les circuits fonctionnant à des fréquences très élevées, comme ceux utilisés dans la radio et la communication sans fil, les effets capacitifs et inductifs peuvent rendre les lois de Kirchhoff moins précises.
• Circuits non-linéaires : Les lois de Kirchhoff supposent une relation linéaire entre le courant et la tension. Dans les circuits avec des composants non-linéaires, comme les diodes ou les transistors, cette supposition n’est pas toujours valide.
• Échelles microscopiques : Aux échelles micro et nano, notamment dans les semi-conducteurs et les nano-dispositifs, les phénomènes quantiques peuvent entraîner des comportements qui ne sont pas entièrement décrits par les lois de Kirchhoff.

Exemples où les lois ne s’appliquent pas

Pour illustrer ces limitations, considérons quelques exemples :

• Transmission de puissance à très longue distance : dans les systèmes de transmission d’électricité sur de longues distances, les effets de la capacité et de l’inductance des lignes de transmission doivent être pris en compte, ce que les lois de Kirchhoff ne font pas directement.
• Circuits avec composants actifs : dans les circuits intégrant des amplificateurs opérationnels ou d’autres composants actifs, les relations entre courant et tension peuvent devenir assez complexes et dépasser le cadre simple des lois de Kirchhoff.

Importance de la modélisation avancée

Ces limitations soulignent l’importance de techniques de modélisation plus avancées dans certaines situations :

• Méthodes numériques : Pour les circuits complexes, en particulier ceux à haute fréquence ou avec des composants non-linéaires, des méthodes de simulation numérique comme SPICE sont souvent utilisées.
• Théories complémentaires : Dans certains cas, d’autres théories comme l’électromagnétisme de Maxwell ou la mécanique quantique sont nécessaires pour une analyse complète.

Perspectives futures et évolutions

L’impact de la technologie sur les Lois de Kirchhoff

Bien que les lois de Kirchhoff soient établies depuis longtemps, les avancées technologiques continuent d’influencer leur application et leur pertinence.

• Miniaturisation des composants : avec la tendance à la miniaturisation en électronique, surtout dans les circuits intégrés et les dispositifs microélectroniques, les lois de Kirchhoff doivent être appliquées avec une précision accrue, tenant compte des effets quantiques et thermiques.
• Nouveaux matériaux et technologies : l’émergence de nouveaux matériaux conducteurs, comme le graphène, et de technologies comme les circuits imprimés flexibles, pose de nouveaux défis et opportunités pour l’application des lois de Kirchhoff.

Recherches actuelles et développements futurs

Les recherches actuelles dans le domaine de l’électronique et de l’électrophysique continuent de tester les limites et d’étendre les applications des lois de Kirchhoff.

• Électronique organique et moléculaire : dans l’électronique organique, où les composants sont basés sur des molécules organiques, les lois de Kirchhoff aident à comprendre les interactions complexes entre les charges électriques et les matériaux organiques.
• Systèmes photoniques et optoélectroniques : dans les domaines de la photonique et de l’optoélectronique, où la lumière est utilisée aux côtés ou à la place de l’électricité, les lois de Kirchhoff sont adaptées pour analyser les interactions entre la lumière et les circuits électriques.

Adaptation et évolution des Lois de Kirchhoff

En conclusion, bien que les lois de Kirchhoff soient un pilier de l’électrocinétique, elles ne sont pas statiques. Leur application évolue avec les progrès technologiques.

• Intégration avec d’autres domaines : l’interconnexion croissante entre l’électronique et d’autres domaines scientifiques et d’ingénierie nécessite une compréhension plus profonde et parfois une réinterprétation des lois de Kirchhoff.
• Formation et éducation : la manière dont les lois de Kirchhoff sont enseignées et comprises doit également évoluer pour refléter ces changements et préparer les futurs ingénieurs et scientifiques à ces défis.

Quelles sont les lois de Kirchhoff ? La conclusion

Résumé des points clés

Dans cet article, nous avons exploré les lois de Kirchhoff, deux principes fondamentaux en électrocinétique qui jouent un rôle crucial dans la compréhension et l’analyse des circuits électriques. La première loi, la loi des nœuds, traite de la conservation de la charge électrique dans les circuits, tandis que la seconde loi, la loi des mailles, est basée sur le principe de conservation de l’énergie.

Ces lois ne sont pas seulement des outils théoriques, elles sont également appliquées dans de nombreux aspects de la technologie moderne, de la conception de circuits imprimés aux systèmes électroniques intégrés. Toutefois, elles ont leurs limites, en particulier dans les circuits à haute fréquence, non-linéaires, ou à des échelles microscopiques.

L’importance continue des Lois de Kirchhoff

En dépit de ces limites, les lois de Kirchhoff restent un pilier de l’électrotechnique. Elles continuent d’être pertinentes même face aux avancées technologiques, s’adaptant et évoluant pour répondre aux besoins de nouvelles applications et de nouveaux matériaux. Leur compréhension est essentielle pour les étudiants et les professionnels en physique et en ingénierie électrique, et elles demeurent un sujet de recherche et de développement actif.

Perspectives d’avenir

L’avenir verra probablement ces lois s’intégrer davantage avec des domaines comme l’électronique organique, la photonique et l’optoélectronique. Cette intégration, ainsi que l’adaptation aux nouvelles technologies, garantira que les lois de Kirchhoff restent pertinentes et utiles pour les générations futures d’ingénieurs et de scientifiques.

Quelles sont les lois de Kirchhoff ? En conclusion, les lois de Kirchhoff sont bien plus que de simples équations ; elles sont le reflet de principes physiques fondamentaux qui continuent de façonner notre compréhension et notre utilisation de l’électricité et de l’électronique dans un monde en constante évolution.